目錄

• 一. 插入排序的定義
• 二. 插入排序的流程
• 三. 插入排序的圖解
• 四. 插入排序的代碼
• 五. 插入排序的時(shí)間復(fù)雜度
• 六. 插入排序的總結(jié)

一. 插入排序的定義

插入排序就像是你打撲克牌，你從牌堆頂取一張牌，找到合適的位置插入到已有牌的順序中，并不斷重復(fù)這一步驟直到所有的牌都被 插入到合適的位置，最終使得整副牌有序。

與打牌類似，插入排序（Insertion sort）的實(shí)現(xiàn)方法是：

• 首先假設(shè)第一個(gè)數(shù)據(jù)是已經(jīng)排好序的，接著取出下一個(gè)數(shù)據(jù)，在已經(jīng)排好序的數(shù)據(jù)中從后往前掃描，找到比它小的數(shù)的位置，將該位置之后的數(shù)整體后移一個(gè)單位，然后再將該數(shù)插入到該位置。
• 不斷重復(fù)上述操作，直到所有的數(shù)據(jù)都插入到已經(jīng)排好序的數(shù)據(jù)中，排序完成。

插入排序的優(yōu)勢在于它的性能表現(xiàn)在已經(jīng)有序的序列上比冒泡排序、選擇排序兩種算法要好。

• 它的時(shí)間復(fù)雜度為O(n)，因此，如果序列已經(jīng)被排好，插入排序?qū)?huì)比冒泡排序和選擇排序快得多。
• 另外，插入排序空間復(fù)雜度為O(1)，因此，對于內(nèi)存限制較小的情況，插入排序也是一個(gè)更優(yōu)的選擇。

二. 插入排序的流程

插入排序的流程如下：

• 首先，假設(shè)數(shù)組的第一個(gè)元素已經(jīng)排好序了，因?yàn)樗挥幸粋€(gè)元素，所以可以認(rèn)為是有序的。
• 然后，從第二個(gè)元素開始，不斷與前面的有序數(shù)組元素進(jìn)行比較。
• 如果當(dāng)前元素小于前面的有序數(shù)組元素，則把當(dāng)前元素插入到前面的合適位置。
• 否則，繼續(xù)與前面的有序數(shù)組元素進(jìn)行比較。
• 以此類推，直到整個(gè)數(shù)組都有序。
• 循環(huán)步驟2~5，直到最后一個(gè)元素。
• 完成排序。

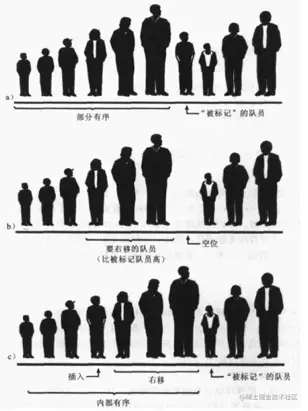
三. 插入排序的圖解

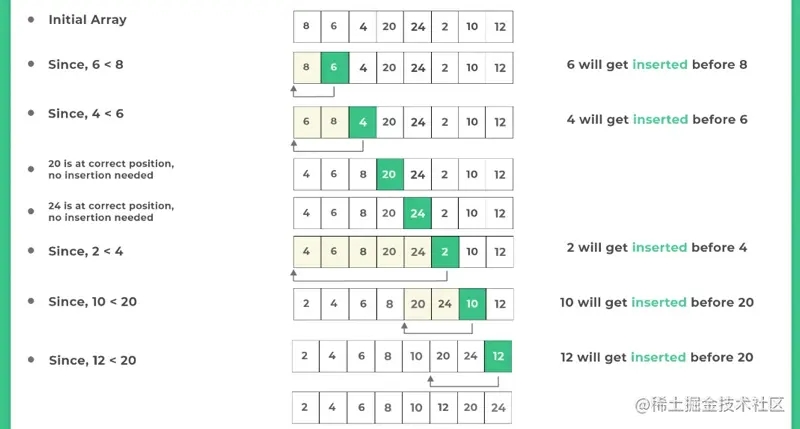
四. 插入排序的代碼

以下是 TypeScript 實(shí)現(xiàn)的插入排序代碼，帶有詳細(xì)的注釋：

function insertionSort(arr: number[]): number[] {  // 對于數(shù)組的每一個(gè)元素，從它開始到0位置，比較該元素和前一個(gè)元素的大小  for (let i = 1; i < arr.length; i++) {    let current = arr[i];    let j = i - 1;    // 如果該元素小于前一個(gè)元素，那么前一個(gè)元素向后移動(dòng)，并繼續(xù)向前比較    while (j >= 0 && arr[j] > current) {      arr[j + 1] = arr[j];      j--;    }    // 如果該元素大于前一個(gè)元素，那么它將放到合適的位置    arr[j + 1] = current;  }  // 返回排序后的數(shù)組  return arr;}// 測試數(shù)據(jù)const testArr = [5, 2, 9, 1, 5, 6];// 調(diào)用插入排序函數(shù)const sortedArr = insertionSort(testArr);// 打印結(jié)果console.log(sortedArr);

代碼執(zhí)行的過程：

• 首先我們定義了一個(gè) insertSort 函數(shù)，并傳入一個(gè)數(shù)字?jǐn)?shù)組作為參數(shù)。
• 接著我們定義一個(gè)變量 current，它將存儲(chǔ)當(dāng)前需要比較的數(shù)字。
• 然后我們使用一個(gè)循環(huán)，將數(shù)組的第二項(xiàng)到最后一項(xiàng)依次與前面的數(shù)字進(jìn)行比較。
• 在內(nèi)層循環(huán)中，我們首先將 j 定義為 i-1，然后每次執(zhí)行循環(huán)時(shí)，如果 j 大于等于 0 并且 arr[j] 大于 current，我們就交換 arr[j] 和 arr[j + 1] 的值。
• 在循環(huán)結(jié)束后，我們將 current 插入到正確的位置，并繼續(xù)比較下一個(gè)數(shù)字。
• 當(dāng)所有數(shù)字都被比較過后，我們就可以返回最終排序好的數(shù)組。

五. 插入排序的時(shí)間復(fù)雜度

插入排序的時(shí)間復(fù)雜度在最好的情況下為O(n)，在最壞的情況下為O(n^2)，平均時(shí)間復(fù)雜度為O(n^2)。

當(dāng)數(shù)據(jù)已經(jīng)有序時(shí)，插入排序只需要做n-1次比較和0次移動(dòng)，運(yùn)行時(shí)間為O(n)；

當(dāng)數(shù)據(jù)完全逆序時(shí)，插入排序需要做n-1趟比較和3/2*(n-1)^2/2次移動(dòng)，運(yùn)行時(shí)間為O(n^2)。

由于插入排序的最好時(shí)間復(fù)雜度與最壞時(shí)間復(fù)雜度都接近O(n^2)，所以插入排序適用于數(shù)據(jù)規(guī)模不大的場合，如果數(shù)據(jù)規(guī)模很大，通常使用其他算法。

六. 插入排序的總結(jié)

• 插入排序是一種簡單而直觀的排序算法，它可以快速地對部分有序的數(shù)組進(jìn)行排序。
• 插入排序通過比較相鄰的元素并在需要時(shí)將其交換，來實(shí)現(xiàn)從小到大的排列。
• 插入排序的時(shí)間復(fù)雜度在最好情況下是線性O(shè)(n)，最壞情況下是O(n^2)。

總而言之，如果數(shù)組部分有序，插入排序可以比冒泡排序和選擇排序更快。

• 但是如果數(shù)組完全逆序，則插入排序的時(shí)間復(fù)雜度比較高，不如快速排序或歸并排序。
• 因此，在選擇排序算法時(shí)，應(yīng)該根據(jù)需要選擇合適的算法。

以上就是TypeScript十大排序算法插入排序?qū)崿F(xiàn)示例詳解的詳細(xì)內(nèi)容，更多關(guān)于TypeScript插入排序算法的資料請關(guān)注其它相關(guān)文章！