文章詳情頁
TypeScript十大排序算法之選擇排序實現示例詳解
瀏覽:44日期:2022-06-01 13:19:17
目錄
- 一. 選擇排序的定義
- 二. 選擇排序的流程
- 三. 選擇排序的圖解
- 四. 選擇排序的代碼
- 五. 選擇排序的時間復雜度
- 六. 選擇排序的總結
一. 選擇排序的定義
選擇排序(Selection Sort)是一種簡單的排序算法。
它的基本思想是:
- 首先在未排序的數列中找到最小(大)元素,然后將其存放到數列的起始位置;
- 接著,再從剩余未排序的元素中繼續尋找最小(大)元素,然后放到已排序序列的末尾。
- 以此類推,直到所有元素均排序完畢。
選擇排序的主要優點與數據移動有關。
- 如果某個元素位于正確的最終位置,則它不會被移動。
- 選擇排序每次交換一對元素,它們當中至少有一個將被移到其最終位置上,因此對n個元素的表進行排序總共進行至多n-1次交換。
- 在所有的完全依靠交換去移動元素的排序方法中,選擇排序屬于非常好的一種。
選擇排序的實現方式很簡單,并且容易理解,因此它是學習排序算法的很好的入門途徑。
二. 選擇排序的流程
選擇排序流程詳細步驟:
- 首先將要排序的數組復制到一個新數組中,這樣原數組不會被改變。
- 初始化最小數字的索引值為0,然后在數組中循環,在當前索引后面的元素中找到最小的數字的索引。
- 如果當前索引位置的數字不是最小數字,那么將這兩個數字互換。
- 繼續尋找下一個數字,直到索引到最后一個元素,此時整個數組已經是從小到大排序的了。
- 重復上面的步驟,每次排序的范圍都會減少一個,直到整個數組排序完畢。

三. 選擇排序的圖解
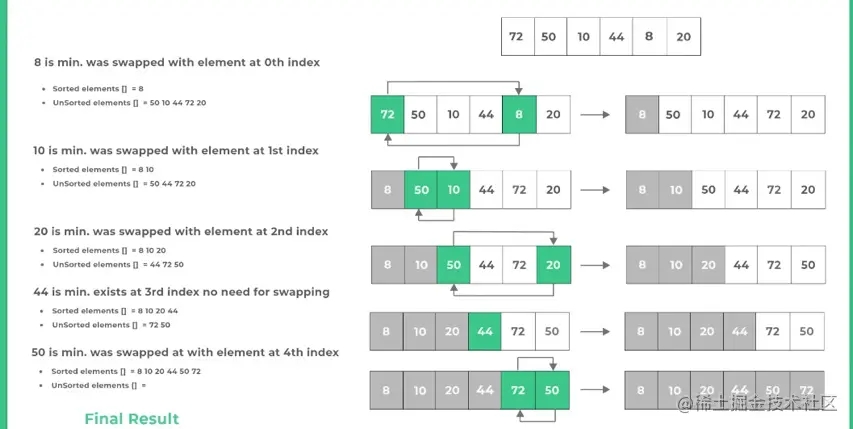

四. 選擇排序的代碼
以下是 TypeScript 實現的選擇排序代碼:
function selectionSort(arr: number[]): number[] { // 循環遍歷整個數組 for (let i = 0; i < arr.length; i++) { // 預設最小數的索引為當前循環的索引 let minIndex = i; // 在后面的數中尋找更小的數 for (let j = i + 1; j < arr.length; j++) { if (arr[j] < arr[minIndex]) {// 如果找到更小的數,記錄它的索引minIndex = j; } } // 如果當前循環的索引不是最小數的索引,交換它們 if (i !== minIndex) { [arr[i], arr[minIndex]] = [arr[minIndex], arr[i]]; } } // 返回排序后的數組 return arr;}// 測試數據const testArr = [5, 2, 9, 1, 5, 6];// 調用插入排序函數const sortedArr = selectionSort(testArr);// 打印結果console.log(sortedArr);以下是代碼的詳細說明:
- 首先循環遍歷整個數組。
- 在每一次循環中,預設最小數的索引為當前循環的索引。
- 在后面的數中尋找更小的數,如果找到更小的數,記錄它的索引。
- 如果當前循環的索引不是最小數的索引,交換它們。
- 重復步驟2-4,直到遍歷完整個數組。
- 返回排序后的數組。
五. 選擇排序的時間復雜度
計算選擇排序算法的時間復雜度,通常是通過分析算法中每一步的執行次數來確定的。
我們分析選擇排序中的每一步,再將每一步的時間復雜度加起來,最后得到的就是選擇排序的時間復雜度。
在選擇排序中,最多的操作是內層循環,其執行了N-1次,并且每次執行內層循環都要花費O(N)的時間。
- 因此,內層循環的時間復雜度是O(N^2)。
外層循環也要執行N-1次,因此,它的時間復雜度也是O(N^2)。
- 所以,整個選擇排序算法的時間復雜度是O(N^2)。
六. 選擇排序的總結
- 選擇排序是一種簡單易懂的排序算法。
- 它的基本思想是遍歷整個列表,每次找出最小的元素,并且將它移到列表的最左邊,重復這個過程直到整個列表都有序排列。
- 在平均情況下,選擇排序的時間復雜度為 O(n^2),在最壞情況下與最好情況下都為 O(n^2)。
- 選擇排序在數據規模較小時非常適用,在數據規模較大時不夠高效。
以上就是TypeScript十大排序算法之選擇排序實現示例詳解的詳細內容,更多關于TypeScript 選擇排序算法的資料請關注其它相關文章!
標簽:
JavaScript
排行榜

 網公網安備
網公網安備