Java基于二分搜索樹、鏈表的實現的集合Set復雜度分析實例詳解
本文實例講述了Java基于二分搜索樹、鏈表的實現的集合Set復雜度分析。分享給大家供大家參考,具體如下:
兩種集合類的復雜度分析在Java底層基于二叉搜索樹實現集合和映射 和Java底層基于鏈表實現集合和映射中以二分搜索樹和鏈表作為底層實現了集合Set,在本節就兩種集合類的復雜度分析進行分析:測試內容:Java底層基于二叉搜索樹實現集合和映射和Java底層基于鏈表實現集合和映射中使用的書籍。測試方法:測試兩種集合類查找單詞所用的時間
//創建一個測試方法 Set<String> set:他們可以是實現了該接口的LinkedListSet和BSTSet對象 private static double testSet(Set<String> set, String filename) { //計算開始時間 long startTime = System.nanoTime(); System.out.println('Pride and Prejudice'); //新建一個ArrayList存放單詞 ArrayList<String> words1 = new ArrayList<>(); //通過這個方法將書中所以單詞存入word1中 FileOperation.readFile(filename, words1); System.out.println('Total words : ' + words1.size()); //增強for循環,定一個字符串word去遍歷words //底層的話會把ArrayList words1中的值一個一個的賦值給word for (String word : words1) set.add(word);//不添加重復元素 System.out.println('Total different words : ' + set.getSize()); //計算結束時間 long endTime = System.nanoTime(); return (endTime - startTime) / 1000000000.0;//納秒為單位 } public static void main(String[] args) { //基于二分搜索的集合 BSTSet<String> bstSet = new BSTSet<>(); double time1 = testSet(bstSet, 'pride-and-prejudice.txt'); System.out.println('BSTSet:' + time1 + 's'); System.out.println('————————————————————'); //基于鏈表實現的集合 LinkedListSet<String> linkedListSet = new LinkedListSet<>(); double time2 = testSet(linkedListSet, 'pride-and-prejudice.txt'); System.out.println('linkedListSet:' + time2 + 's'); }
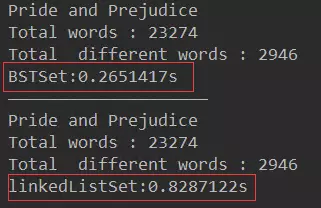
結果:BSTSet的速度比LinkedListed的速度快

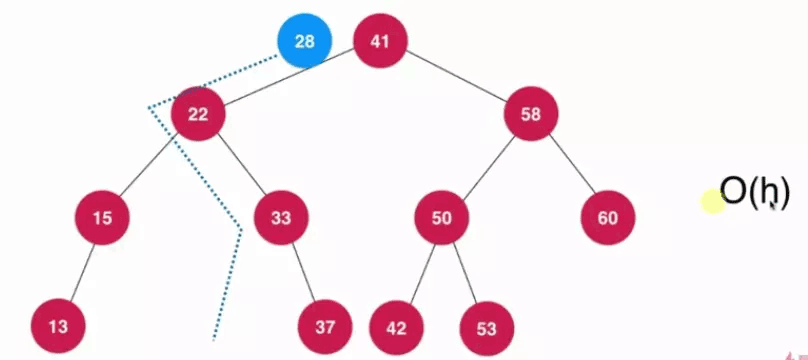
在基于二叉搜索樹的情況下,增加、查詢、刪除的與二叉搜索樹的深度有關,每次操作均為從根節點到某一一支子樹的葉子節點之間進行操作,時間復雜度為0(h),h表示二叉搜索樹的高度(層數)。
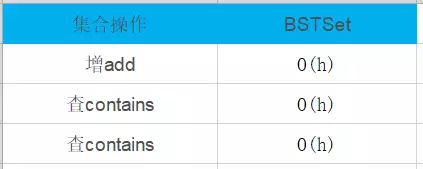
二叉搜索樹復雜度如下:
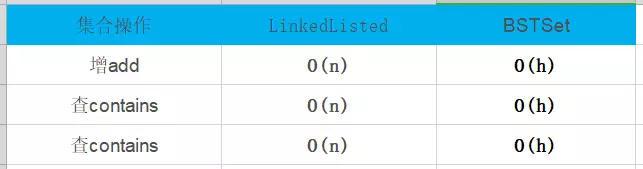
下面對n與h關系進行推導:
2.1.1 采用滿二叉樹的情況進行分析(最優情況)
采用滿二叉樹(每個節點都有左右節點,除了葉子節點)來進行分析的原因為滿二叉樹是一種極端情況,如下圖:

從上圖中關于h層總共有多少個節點有如下推導:

假設節點個數為n個則有如下關系:

針對都是log級別的關系,底數是多少不影響它是log級別的則有:
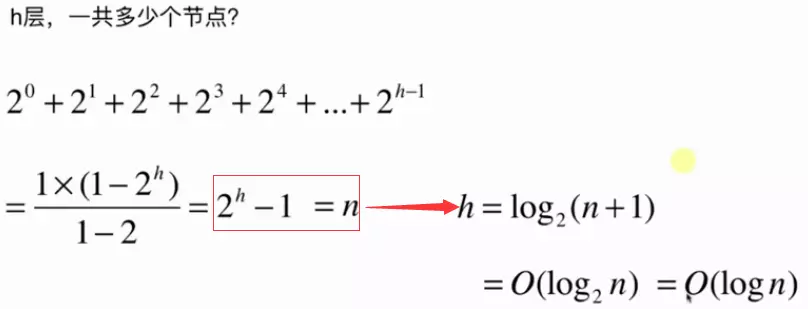
2.1.2 單個孩子情況----二叉搜索樹最壞情況(節點數等于其高度)
比如:下面這種二叉搜索樹
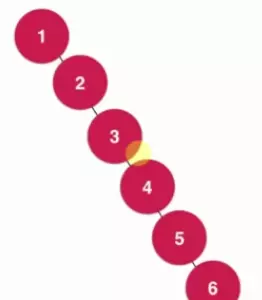
對于這種只有單個孩子的情況,此時二叉搜索樹退化成了鏈表,此時的時間復雜度為O(n)。
2.2 兩種集合復雜度統計
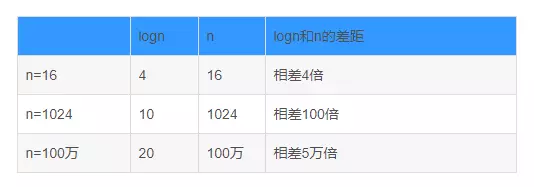
2.2.1 logn和n的差距
推薦是最好的支持,關注是最大的鼓勵。親愛的朋友,很榮幸在園子里遇到您。
本節涉及的源碼地址為https://github.com/FelixBin/dataStructure/tree/master/src/SetPart
更多關于java算法相關內容感興趣的讀者可查看本站專題:《Java數據結構與算法教程》、《Java操作DOM節點技巧總結》、《Java文件與目錄操作技巧匯總》和《Java緩存操作技巧匯總》
希望本文所述對大家java程序設計有所幫助。
相關文章:
 網公網安備
網公網安備