1、流程

大體流程如下，無論圖像、聲音、ADC數(shù)據(jù)都是如下流程：

（1）將原信號進(jìn)行FFT;

（2）將進(jìn)行FFT得到的數(shù)據(jù)去掉需要濾波的頻率；

（3）進(jìn)行FFT逆變換得到信號數(shù)據(jù)；

2、算法仿真

2.1 生成數(shù)據(jù)：

#采樣點選擇1400個，因為設(shè)置的信號頻率分量最高為600Hz，根據(jù)采樣定理知采樣頻率要大于信號頻率2倍，所以這里設(shè)置采樣頻率為1400Hz（即一秒內(nèi)有1400個采樣點）x=np.linspace(0,1,1400)#設(shè)置需要采樣的信號，頻率分量有180，390和600y=2*np.sin(2*np.pi*180*x) + 3*np.sin(2*np.pi*390*x)+4*np.sin(2*np.pi*600*x)

2.2 對生成的數(shù)據(jù)進(jìn)行FFT變換

yy=fft(y) #快速傅里葉變換yf=abs(fft(y))# 取模yf1=abs(fft(y))/((len(x)/2)) #歸一化處理yf2 = yf1[range(int(len(x)/2))] #由于對稱性，只取一半?yún)^(qū)間

2.3顯示轉(zhuǎn)換結(jié)果：

顯示原始FFT模值：

#混合波的FFT（雙邊頻率范圍）plt.figure(2)plt.plot(xf,yf,’r’) #顯示原始信號的FFT模值plt.title(’FFT of Mixed wave(two sides frequency range)’,fontsize=7,color=’#7A378B’) #注意這里的顏色可以查詢顏色代碼表

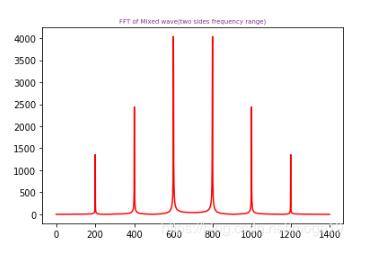
顯示原始FFT歸一化后的模值：

#混合波的FFT（歸一化）plt.figure(3)plt.plot(xf1,yf1,’g’)plt.title(’FFT of Mixed wave(normalization)’,fontsize=9,color=’r’)

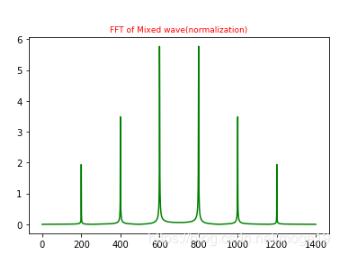
由于對稱，只取一半?yún)^(qū)間進(jìn)行顯示

plt.figure(4)plt.plot(xf2,yf2,’b’)plt.title(’FFT of Mixed wave)’,fontsize=10,color=’#F08080’)

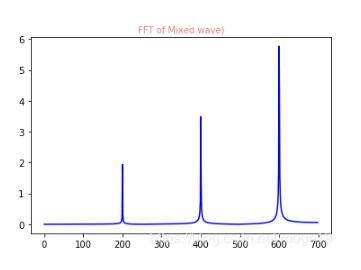
3、利用FFT進(jìn)行濾波

例如將頻率為600HZ的噪聲濾掉，這里直接將該頻段的數(shù)據(jù)置零：

yy=fft(y) #快速傅里葉變換yreal = yy.real# 獲取實數(shù)部分yimag = yy.imag# 獲取虛數(shù)部分test_y =yyfor i in range(len(yy)): if i <=900 and i>=500: test_y[i]=0

對置零后的數(shù)據(jù)進(jìn)行逆變換：

test = np.fft.ifft(test_y) #對變換后的結(jié)果應(yīng)用ifft函數(shù)，應(yīng)該可以近似地還原初始信號。

對還原的數(shù)據(jù)進(jìn)行FFT變換的結(jié)果：

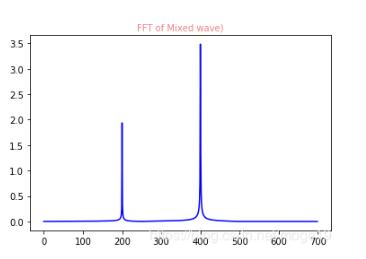
濾波后的數(shù)據(jù)和原數(shù)據(jù)相對比:

藍(lán)色的為原數(shù)據(jù)，橙色的為濾波后的數(shù)據(jù)

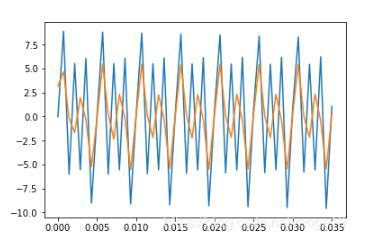
假設(shè)將400Hz和600Hz的信號都濾掉得到的信號圖像如下：

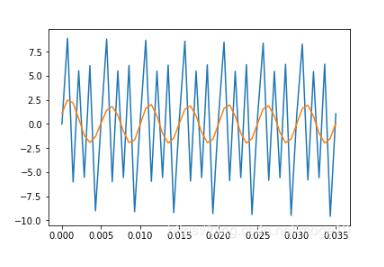
4、對隨機(jī)噪聲進(jìn)行濾波

源碼：

noise_size = 1400noise_array = np.random.normal(0, 2, noise_size) adc_value=[] for i in range(noise_size): adc_value.append(0) y= np.array(adc_value) + noise_arrayyy=fft(y) #快速傅里葉變換yf=abs(fft(y))# 取模yf1=abs(fft(y))/((len(y)/2)) #歸一化處理yf2 = yf1[range(int(len(y)/2))] #由于對稱性，只取一半?yún)^(qū)間#混合波的FFT（雙邊頻率范圍）xf = np.arange(len(y)) plt.figure(1)plt.plot(xf,yf,’r’) #顯示原始信號的FFT模值plt.title(’FFT of Mixed wave(two sides frequency range)’,fontsize=7,color=’#7A378B’) #注意這里的顏色可以查詢顏色代碼表yy=fft(y) #快速傅里葉變換yreal = yy.real# 獲取實數(shù)部分yimag = yy.imag# 獲取虛數(shù)部分test_y =yyfor i in range(len(yy)): if i <=1200 and i>=200: test_y[i]=0test = np.fft.ifft(test_y) #對變換后的結(jié)果應(yīng)用ifft函數(shù)，應(yīng)該可以近似地還原初始信號。y=testyy=fft(y) #快速傅里葉變換yf=abs(fft(y))# 取模yf1=abs(fft(y))/((len(y)/2)) #歸一化處理yf2 = yf1[range(int(len(y)/2))] #由于對稱性，只取一半?yún)^(qū)間#混合波的FFT（雙邊頻率范圍）xf = np.arange(len(y)) plt.figure(2)plt.plot(xf,yf,’r’) #顯示原始信號的FFT模值plt.title(’FFT of Mixed wave(two sides frequency range)’,fontsize=7,color=’#7A378B’) #注意這里的顏色可以查詢顏色代碼表

運行結(jié)果：

原數(shù)據(jù)頻譜圖：

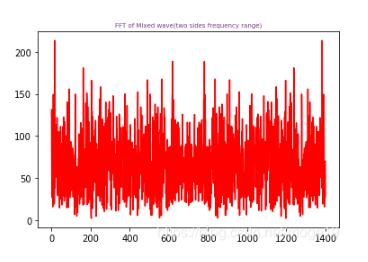
濾波后的頻譜圖：

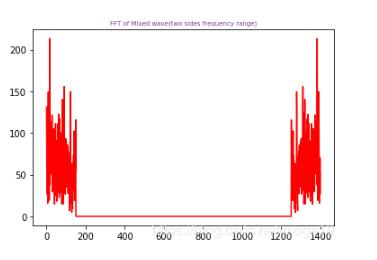
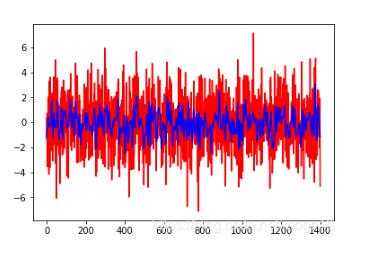
濾波后（藍(lán)色線）與原數(shù)據(jù)（紅色線）對比：

以上這篇Python利用FFT進(jìn)行簡單濾波的實現(xiàn)就是小編分享給大家的全部內(nèi)容了，希望能給大家一個參考，也希望大家多多支持好吧啦網(wǎng)。