淺談Python里面None True False之間的區別
None雖然跟True False一樣都是布爾值。
雖然None不表示任何數據,但卻具有很重要的作用。
它和False之間的區別還是很大的!
例子:
>>> t = None>>> if t:... print('something')... else:... print('nothing')...nothing

區分None和False.使用is來操作!
>>> if t is None:... print('this is None!')... else:... print('this is ELSE!')...this is None!>>>
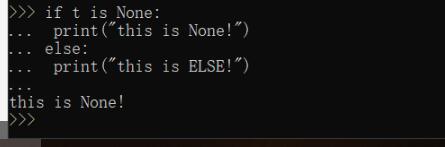
雖然是個小小的區別!但是在Python里面是重要的。你需要將None和不含任何值的空數據結構區分開。
0值的整型/浮點型,空字符串(‘ ’),空列表([]),空元組({}),空集合(set())都是等價于False,但是不等于None。
現在,寫一個函數:
>>> def oj(t):... if t is None:... print('this is None')... elif t:... print('this is True')... else:... print('this is False')...
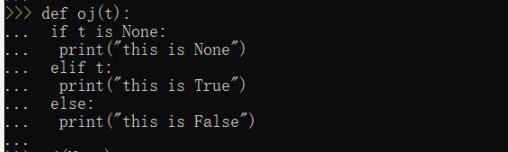
進行數據測驗:
>>> oj(None)this is None>>> oj(True)this is True>>> oj(False)this is False>>> oj(0)this is False>>> oj(0.0)this is False>>> oj([])this is False>>> oj(())this is False>>> oj({})this is False

以上說明,None,False,True還是有很大不同的~
補充知識:python '0.3 == 3 * 0.1' 為False的原因
一.引入
如果你在你的解釋器中輸入以下第一行代碼:
>>> 0.3 == 3 * 0.1
False
你會發現,輸出為False。
對于CS小白而言,對此表示費解。
因此我查了相關的資料,進行了一下總結。
二.浮點算法的問題和局限
1.計算機硬件對于浮點數的處理方式
首先,我們必須明白一件事情。浮點數在計算機硬件中表示為基數2(二進制)的分數。
例如:
0.125(10) == 1/10 + 2/100 + 5/1000
0.001(2) == 0/2 + 0/4 + 0/8
這兩個分數具有相同的值,唯一的實際區別是,第一個分數以10為基數的分數表示,第二個分數以2為基數。當我們輸入0.125時,計算機硬件會以第二種方式表示,而不是第一種。
但是不幸的是,大多數十進制分數不能完全表示為二進制分數。
結果是,通常我們輸入的十進制浮點數僅由計算機中實際存儲的二進制浮點數
近似。但是在十進制不能完全表示為二進制分數的情況下,無論多么近似,終究不是確切值。
2.例子:對于0.1的處理
例如0.1(10),無論我們愿意使用多少個2位數字,十進制值0.1都不能精確表示為2進制小數,即以2為底的1/10是無限重復的分數。
0.1(10) == 0.0001100110011001100110011001100110011001100110011...(2)
當我們讓它停在某個有限的位數,就可以得出一個近似值。
因為Python浮點數可使用 53位精度 ,
因此輸入十進制數時計算機內部存儲的值0.1是
0.00011001100110011001100110011001100110011001100110011010(2)
這個值接近但是不等于1/10.
這也是造成print(0.3 == 3 * 0.1)輸出為False的原因。
如果要強制使用python輸出計算機內保存的0.1的真實十進制值,應該為
>>> 0.1
0.1000000000000000055511151231257827021181583404541015625
由于這一串數字實在太長了,所以Python通過顯示舍入的值來保持數字的可管理性。所以實際上我們看到是:
>>> 0.1
0.1
但是我們要明白,機器中的值不完全是1/10,這只是舍入了真實機器值的顯示。
3.一點有趣的東西
上面我們提到了Python通過顯示舍入的值來保持數字的可管理性,我們看到的只是舍入了真實機器值的顯示。通過下面的例子,我們就可以更加清楚這一事實。
當我們用python寫下下面的代碼時,就會發現這個神奇的現象。
這本質上是二進制浮點數:這不是Python中的bug,也不是代碼中的bug。在支持硬件浮點算術的所有語言中,都會看到同一種東西(盡管某些語言在默認情況下或在所有輸出模式下可能不會顯示差異)。
1)0.1+0.2
>>> 0.1 + 0.2
0.30000000000000004
2)round(2.675, 2)
i)round( x [, n] )的用法
作用: 返回浮點數x的四舍五入值。
參數:
x ? 數值/數值表達式。
n ? 要保留的小數位數,可以省略。若省略,n默認為0,即四舍五入到整數。
ii)round( 2.675, 2)
按照我們的邏輯來看,輸入round( 2.675, 2 ),輸出應該為2.68。但是實際上是:
>>> round(2.675, 2)
2.67
三.表示錯誤(選讀)
在這里我們詳細說明“ 0.1”示例,并說明我們如何自己對此類情況進行準確的分析。如果你不想深究其背后的原因,下面的可以忽略。
1.表示錯誤的概念、影響和原因
(1)概念
表示錯誤是指某些(在實際中為大多數)小數部分不能完全表示為二進制(基數為2)分數。
(2)影響
使得Python(或Perl,C,C ++,Java,Fortran和其他許多語言)經常不顯示我們所期望的確切十進制數字。
(3)原因
如今,幾乎所有機器都使用IEEE-754浮點算法,并且幾乎所有平臺都將Python浮點數映射到IEEE-754“雙精度”。754個double包含53位精度,因此在輸入時,計算機會努力將浮點數轉換為J / 2 ** N形式的最接近分數, 其中J是一個正好包含53位的整數。
2.'0.1'的具體分析
轉化目標:1 / 10 ~= J / (2 ** N)
所以:J ~= 2 ** N / 10
1)求解N
因為J是一個正好包含53位的整數(但是實際上最后我們用的是J的近似值( >=2 ** 52 and < 2 ** 53)是通過N計算出來的),并且N是一個整數,所以我們可以得到N的最佳值是56
>>> 2**524503599627370496>>> 2**539007199254740992>>> 2**56/107205759403792793
2)求解我們要用的J的近似值
我們通過N來求解實際的J,我們實際上用的J其實是(2**N /10)四舍五入之后的值。
i)divmod(a, b)
功能: 接收兩個數字類型(非復數)參數,返回一個包含商和余數的元組(a // b, a % b)。
參數:
a ? 被除數
b ? 除數
ii)求解J近似值
>>> q, r = divmod(2**56, 10)>>> r6
因為余數為6>5,所以我們用的J的近似值是
>>> q+1
7205759403792794
3)求解'0.1'的近似值
因此,在754倍精度中,最接近1/10的最佳近似值是
7205759403792794 / 72057594037927936
【注】由于我們四舍五入,因此實際上比1/10大一點;如果我們不進行四舍五入,則商將小于1/10。但是在任何情況下都不能完全是 1/10!
4)獲取計算機存儲值
通過上面的分析,我們可以看到計算機永遠不會“看到” 1/10:它看到的是上面給出的精確分數,它可以得到的最佳754倍近似值(即J的近似值)
>>> .1 * 2**56
7205759403792794.0
如果我們將該分數乘以10 ** 30,我們可以看到其30個最高有效十進制數字的(截斷)值:
>>> 7205759403792794 * 10**30 // 2**56
100000000000000005551115123125L
在Python 2.7和Python 3.1之前的版本中,Python將該值四舍五入為17個有效數字,即為’0.10000000000000001’。
在最新版本中,Python會基于最短的十進制分數顯示一個值,該值會正確舍入為真實的二進制值,并僅得出’0.1’。
以上這篇淺談Python里面None True False之間的區別就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持好吧啦網。
相關文章:

 網公網安備
網公網安備