利用Python實現最小二乘法與梯度下降算法
%matplotlib inlineimport sympyimport numpy as npimport matplotlib.pyplot as pltfrom sympy.abc import x as a,y as b生成模擬數據
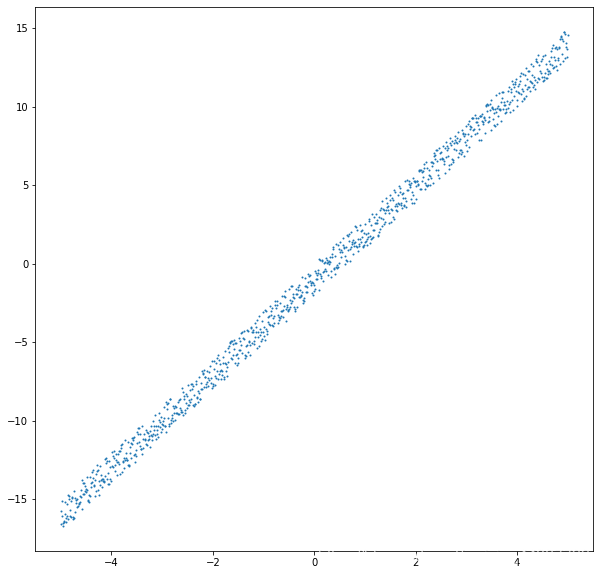
# 模擬函數 y=3x-1#自變量x=np.linspace(-5,5,num=1000)#加入噪聲noise=np.random.rand(len(x))*2-1#因變量y=3*x-1+noise查看所生成數據的圖像
plt.figure(figsize=(10,10))plt.scatter(x,y,s=1)
y=ax+b #目標函數e=1/2*Σ([axi+b]-yi)^2 #代價函數,求使得代價函數為最小值時,對應的a和b對a求偏導->Σ(axi+b-yi)*xi對b求偏導->Σ(axi+b-yi)1. 通過最小二乘法求a,b
我們知道當在a,b處的偏導為0時,代價函數e達到最小值,所以得到二元一次方程組
Σ(axi+b-yi)*xi=0Σ(axi+b-yi)=0
該方程組是關于未知數為a,b的二元一次方程組,通過求解該方程,得到a,b
result=sympy.solve([ np.sum((a*x+b-y)*x), np.sum(a*x+b-y)],[a,b])print(result)#{x: 3.01182977621975, y: -1.00272253325765}
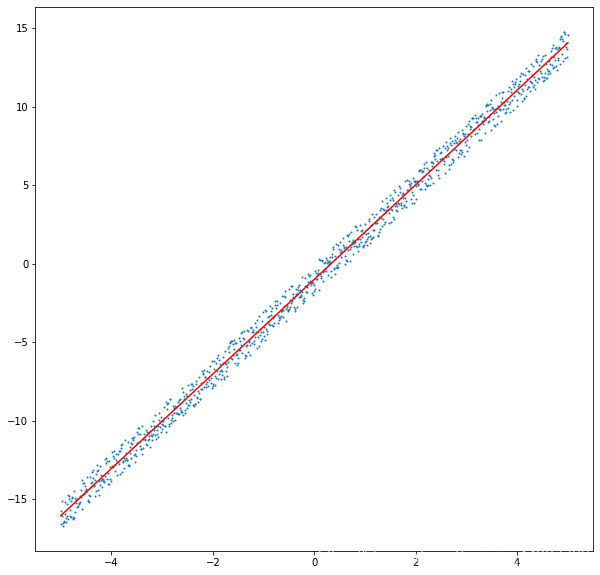
通過sympy庫解方程組,得出了a= 3.01182977621975,b= -1.00272253325765,已經與我們真實的a,b很接近了,下面進行作圖
plt.figure(figsize=(10,10))plt.scatter(x,y,s=1)plt.plot(x,result[a]*x+result[b],c=’red’)print(type(a),type(b))#<class ’sympy.core.symbol.Symbol’> <class ’sympy.core.symbol.Symbol’>
我們注意到最小二乘法最后一步要求p個方程組,是非常大的計算量,其實計算起來很難,因此我們就有了一種新的計算方法,就是梯度下降法,梯度下降法可以看作是 更簡單的一種 求最小二乘法最后一步解方程 的方法
# 注意這里覆蓋了sympy.abc的a和b# 設定a和b的起始點a,b=0.1,0.1#步長,也稱作學習率alpha=0.00001#循環一千次結束for i in range(1000): a-=alpha*np.sum((a*x+b-y)*x) b-=alpha*np.sum(a*x+b-y)print(a,b)#3.0118297762197526 -1.002674927350334
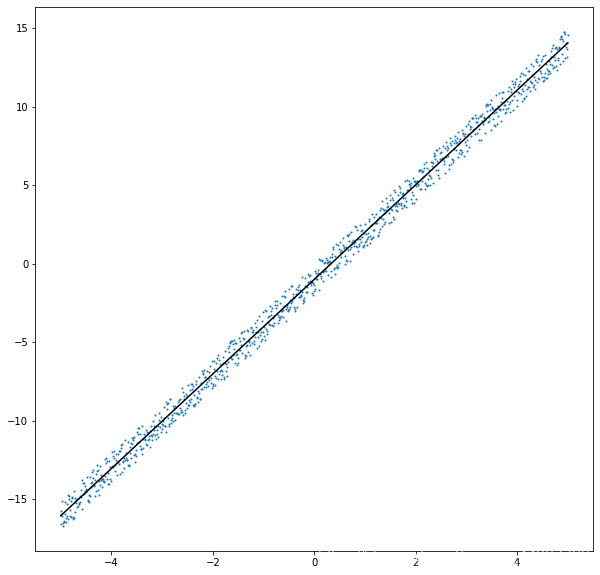
通過梯度下降法,得出了a= 3.0118297762197526,b= -1.002674927350334,也是很接近真實的a,b值了,作圖看看
plt.figure(figsize=(10,10))plt.scatter(x,y,s=1)plt.plot(x,a*x+b,c=’black’)print(type(a),type(b))#<class ’numpy.float64’> <class ’numpy.float64’>
到此這篇關于利用Python實現最小二乘法與梯度下降算法的文章就介紹到這了,更多相關Python最小二乘法與梯度下降內容請搜索好吧啦網以前的文章或繼續瀏覽下面的相關文章希望大家以后多多支持好吧啦網!
相關文章:
 網公網安備
網公網安備